无人机镜头畸变校正是计算机视觉和摄影测量领域的关键技术,主要用于消除由于镜头光学特性导致的图像变形,提升图像质量和测量精度,镜头畸变主要分为径向畸变和切向畸变,其中径向畸变由镜头形状不规则引起,表现为桶形或枕形变形;切向畸变则由镜头与传感器安装误差导致,表现为图像局部区域的偏移,畸变校正的核心是通过数学模型描述畸变规律,并利用校正公式对原始图像进行像素坐标变换,从而恢复图像的真实几何关系。

径向畸变的校正公式通常采用多项式模型,其表达式为:
[ x{\text{corrected}} = x{\text{distorted}} (1 + k_1 r^2 + k_2 r^4 + k3 r^6) ]
[ y{\text{corrected}} = y_{\text{distorted}} (1 + k_1 r^2 + k_2 r^4 + k3 r^6) ]
((x{\text{distorted}}, y{\text{distorted}}))为畸变图像像素坐标,((x{\text{corrected}}, y{\text{corrected}}))为校正后坐标,(r = \sqrt{(x{\text{distorted}} - cx)^2 + (y{\text{distorted}} - c_y)^2})为像素点到图像中心的归一化距离,((c_x, c_y))为图像主点坐标,(k_1, k_2, k_3)为径向畸变系数,高阶项(如(r^4, r^6))用于描述非线性畸变,通常在广角镜头校正中需要保留。
切向畸变的校正公式引入了切向畸变系数(p_1, p2),其表达式为:
[ \Delta x{\text{tangential}} = 2 p_1 x y + p2 (r^2 + 2x^2) ]
[ \Delta y{\text{tangential}} = p_1 (r^2 + 2y^2) + 2 p2 x y ]
校正后的坐标需叠加切向畸变修正量:
[ x{\text{corrected}} = x_{\text{distorted}} (1 + k_1 r^2 + k_2 r^4 + k3 r^6) + \Delta x{\text{tangential}} ]
[ y{\text{corrected}} = y{\text{distorted}} (1 + k_1 r^2 + k_2 r^4 + k3 r^6) + \Delta y{\text{tangential}} ]
切向畸变通常较小,但在高精度应用中(如无人机测绘)不可忽略。
综合径向和切向畸变的完整校正公式可表示为:
[ x{\text{corrected}} = x{\text{distorted}} + (x_{\text{distorted}} - c_x) (k_1 r^2 + k_2 r^4 + k3 r^6) + \Delta x{\text{tangential}} ]
[ y{\text{corrected}} = y{\text{distorted}} + (y_{\text{distorted}} - c_y) (k_1 r^2 + k_2 r^4 + k3 r^6) + \Delta y{\text{tangential}} ]
该公式通过像素坐标的平移和缩放实现畸变校正,其中畸变系数((k_1, k_2, k_3, p_1, p_2))和主点坐标((c_x, c_y))需通过相机标定实验获取,常用标定方法包括张正友标定法和基于三维靶标的标定法。
实际应用中,无人机镜头畸变校正的流程可分为三步:
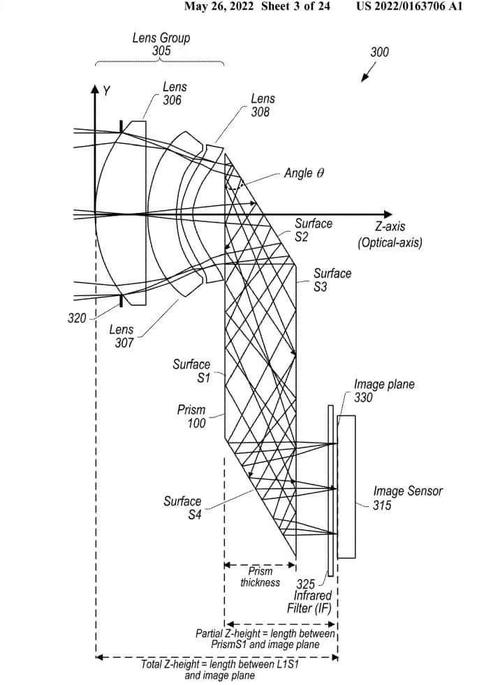
- 标定参数获取:使用标定板拍摄多角度图像,通过最小二乘法优化求解畸变系数和内参矩阵。
- 坐标变换计算:对图像中每个像素点,根据上述公式计算校正后的坐标。
- 像素重映射:通过双线性插值法处理非整数坐标点,避免信息丢失。
以下为畸变校正参数示例表(假设基于某无人机广角镜头标定结果):
| 参数类型 | 参数符号 | 数值范围示例 | 物理意义 |
|---|---|---|---|
| 径向畸变系数 | (k_1) | -0.2~0.2 | 二阶径向畸变强度 |
| 径向畸变系数 | (k_2) | -0.01~0.01 | 四阶径向畸变强度 |
| 径向畸变系数 | (k_3) | -0.001~0.001 | 六阶径向畸变强度 |
| 切向畸变系数 | (p_1) | -0.001~0.001 | 切向畸变水平方向修正量 |
| 切向畸变系数 | (p_2) | -0.001~0.001 | 切向畸变垂直方向修正量 |
| 主点坐标 | (c_x) | 图像宽度/2 | 光学中心在图像中的x坐标 |
| 主点坐标 | (c_y) | 图像高度/2 | 光学中心在图像中的y坐标 |
需要注意的是,畸变校正效果受标定精度、镜头温度变化和无人机振动等因素影响,在实时处理中,可采用GPU加速优化坐标变换效率,例如通过CUDA并行计算提升处理速度,对于大畸变镜头(如鱼眼镜头),可能需要采用分段校正或非多项式模型(如立体投影模型)以进一步提高精度。
相关问答FAQs
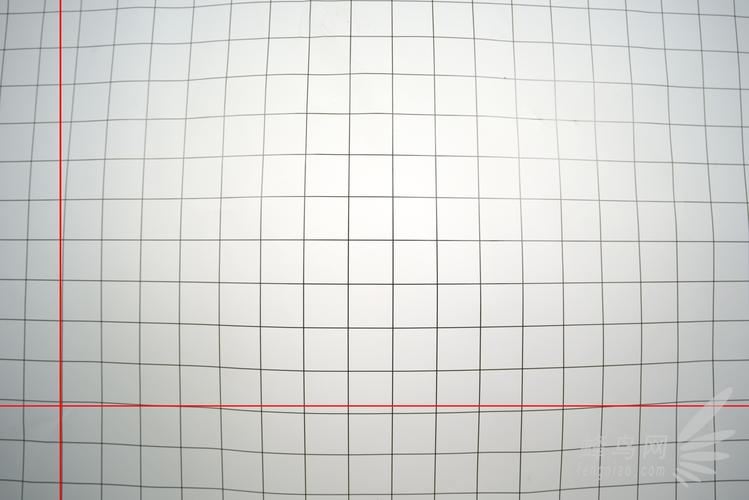
Q1:无人机镜头畸变校正后,图像边缘会出现黑色区域,如何处理?
A:黑色区域是由于校正后图像坐标系超出原始图像范围导致的,解决方法包括:(1)在坐标变换时裁剪有效区域,保留无黑边部分;(2)通过图像填充算法(如边缘复制或镜像填充)扩展图像边界;(3)调整畸变模型阶数或标定参数,减少边缘变形幅度,实际应用中,通常结合裁剪和填充技术平衡校正效果与图像完整性。
Q2:畸变系数标定不准确会对无人机测绘精度产生多大影响?
A:畸变系数标定误差会直接导致像素坐标转换偏差,进而影响测绘精度,径向畸变系数(k_1)误差0.01可能在图像边缘(距离中心800像素处)引入约6.4像素的位置误差(假设像素尺寸为5μm,相当于32μm的地面误差),对于大比例尺测绘(如1:500),可能超过允许误差范围,因此需通过高精度标定板(如棋盘格间距≤1mm)和多角度标定图像确保参数准确性。